Questão 16 - 1ª Fase - IME 2025

Poliedro Resolve - Resolução IME 1ª Fase 2025

Poliedro Resolve Resolução - IME 2ª Fase Dia 1 - 2025

Poliedro Resolve Resolução - IME 2ª Fase Dia 2 - 2025

Selecione uma prova

Gabarito

1ª Fase
1. 1C
2. 2E
3. 3B
4. 4C
5. 5D
6. 6E
7. 7D
8. 8D
9. 9A
10. 10B
11. 11C
12. 12B
13. 13A
14. 14D
15. 15E
16. 16A
17. 17C
18. 18D
19. 19B
20. 20A
21. 21A
22. 22E
23. 23B
24. 24E
25. 25D
26. 26D
27. 27A
28. 28C
29. 29D
30. 30C
31. 31D
32. 32C
33. 33A
34. 34C
35. 35D
36. 36D
37. 37E
38. 38B
39. 39B
40. 40E

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 16

Objetiva

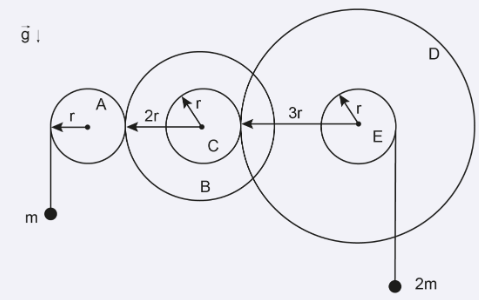
Cinco discos A, B, C, D e E, de centros fixos, giram solidariamente conforme a geometria da figura. Duas partículas de massas m e 2m enrolam ou desenrolam fios inextensíveis às mesmas velocidades escalares das bordas de seus respectivos discos.

Dados:

aceleração da gravidade: g;

Observações:

os cinco discos estão inicialmente em repouso;
os cinco centros dos discos estão na mesma horizontal;
o disco A está engrenado ao disco B;
ao girar, o disco B faz o disco C girar à mesma velocidade angular, pois B e C são concêntricos;
o disco C está engrenado ao disco D;
ao girar, o disco D faz o disco E girar à mesma velocidade angular, pois D e E são concêntricos;
a partícula de menor massa está associada ao disco A e a de maior massa ao disco E;
despreze as massas dos discos e desconsidere quaisquer deslizamentos.

Pelo princípio da conservação da energia, a aceleração (módulo e sentido) da partícula de maior massa, após o início de seu movimento, é:

Alternativas

A
$\frac{2}{19} g$ , de baixo para cima (enrolando o fio)
B
$\frac{2}{19} g$ , de cima para baixo (desenrolando o fio)
C
$\frac{4}{19} g$ , de baixo para cima (enrolando o fio)
D
$\frac{4}{11} g$ , de cima para baixo (desenrolando o fio)
E
$\frac{4}{11} g$ , de baixo para cima (enrolando o fio)

Gabarito:
A

Dos acoplamentos, têm-se as seguintes relações:

$ω_{A} \cdot r = ω_{B} \cdot 2 r \Rightarrow ω_{A} = 2 ω_{B} ω_{B} = ω_{C} ω_{C} \cdot r = ω_{D} \cdot 3 r \Rightarrow ω_{D} = \frac{ω_{C}}{3} ω_{E} = ω_{D}$

Portanto,

$ω_{A} = 6 ω_{E} \Rightarrow \frac{v_{A}}{r} = 6 \cdot \frac{v_{E}}{r} \Rightarrow v_{A} = 6 v_{E}$

Note que $v_{A}$ é a velocidade da massa $m_{1}$ e $v_{E}$ , a velocidade da massa 2m.

Portanto, da cinemática, a mesma razão de 1:6 deve se manter entre os deslocamentos e as acelerações de A e E.

Suponha-se que a massa m desça, e a massa 2m suba. Diagrama de forças:

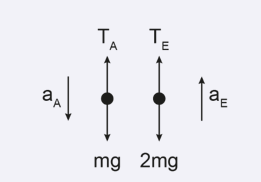
2ª Lei de Newton para as massas:

$mg - T_{A} = {ma}_{A} (I) T_{E} - 2 mg = 2 m a_{E} (II)$

Mas, da cibernética, $a_{A} = 6 a_{A} (III)$ .

E, para que haja conservação de energia, o trabalho total realizado pelas trações deve ser zero:

$+ T_{E} \cdot x_{E} - T_{A} \cdot x_{A} = 0 \Rightarrow + T_{E} \cdot x_{E} - T_{A} \cdot 6 x_{E} = 0 \Rightarrow T_{E} = 6 T_{A} (IV)$

De (I), (II), (III) e (IV):

$4 mg = 36 m a_{E} + 2 m a_{E} \Rightarrow a_{E} = \frac{2 g}{19} (↓)$

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!