Questão 23 - 1ª Fase - IME 2025

Poliedro Resolve - Resolução IME 1ª Fase 2025

Poliedro Resolve Resolução - IME 2ª Fase Dia 1 - 2025

Poliedro Resolve Resolução - IME 2ª Fase Dia 2 - 2025

Selecione uma prova

Gabarito

1ª Fase
1. 1C
2. 2E
3. 3B
4. 4C
5. 5D
6. 6E
7. 7D
8. 8D
9. 9A
10. 10B
11. 11C
12. 12B
13. 13A
14. 14D
15. 15E
16. 16A
17. 17C
18. 18D
19. 19B
20. 20A
21. 21A
22. 22E
23. 23B
24. 24E
25. 25D
26. 26D
27. 27A
28. 28C
29. 29D
30. 30C
31. 31D
32. 32C
33. 33A
34. 34C
35. 35D
36. 36D
37. 37E
38. 38B
39. 39B
40. 40E

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 23

Objetiva

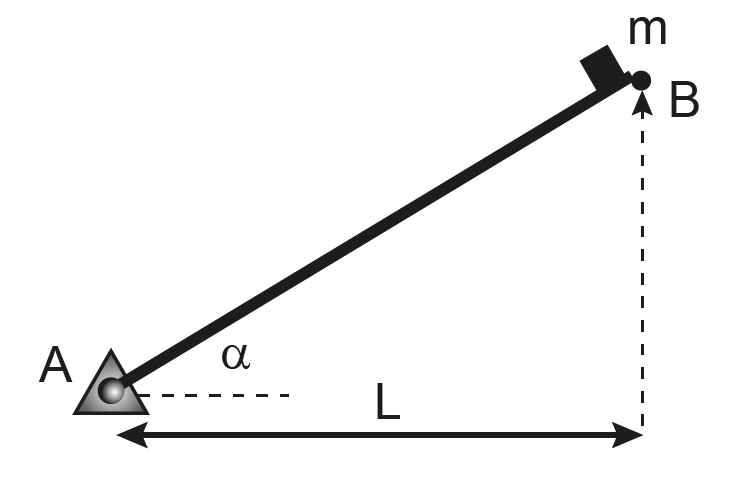
A figura mostra uma rampa inclinada, de massa desprezível, apoiada por dois suportes fixados nos pontos A e B. O apoio em A admite forças horizontais e verticais e o apoio em B apenas forças verticais. Um objeto de dimensões desprezíveis é liberado do ponto B a partir do repouso e se desloca sem atrito em direção a A.

Dados:

aceleração da gravidade: g;
massa do objeto: m;
ângulo da rampa com a horizontal: $α$ ;
comprimento horizontal da rampa: L.

O módulo da reação de apoio em A quando o objeto estiver passando pelo meio da rampa é igual a:

Alternativas

A
$\frac{1}{2} mg (cosα + senα)$
B
$\frac{1}{2} mg$
C
$\frac{1}{2} mg cosα \sqrt{\cos^{2} α + \frac{1}{2} {sen}^{2} α}$
D
$\frac{1}{2} mg cosα \sqrt{\cos^{2} α + \frac{1}{4} {sen}^{2} α}$
E
$\frac{1}{2} mg cosα$

Gabarito:
B

Resolução 1

Quando o objeto está no meio da rampa, a força $mg cosα$ fica aplicada no ponto médio de AB.

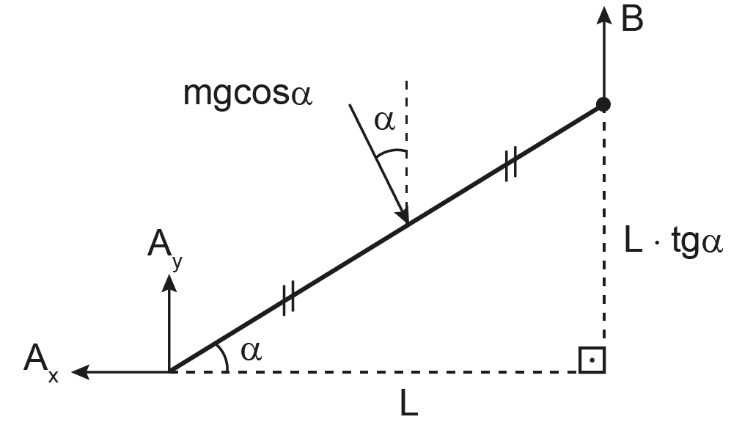
Equilíbrio na direção horizontal:

$A_{x} = mg cosα \cdot senα \Rightarrow A_{x} = mg cosα senα$

Equilíbrio de torques em relação a B:

$mg cosα \cdot (\frac{1}{2} \cdot \frac{L}{\cos α}) = A_{x} \cdot Ltgα + A_{y} \cdot L \frac{mg}{2} = mg senα cosα \frac{senα}{cosα} + A_{y} A_{y} = mg (\frac{1}{2} - {sen}^{2} α)$

Portanto, a reação pedida vale:

$A^{2} = A_{x}^{2} + A_{y}^{2}$

$A^{2} = {(mg)}^{2} ({sen}^{2} α \cos^{2} α + \frac{1}{4} - {sen}^{2} α + {sen}^{4} α) A = mg \sqrt{{sen}^{2} α \underset{⏟}{(\cos^{2} α + {sen}^{2} α)} + \frac{1}{4} - {sen}^{2} α}_{1} A = mg \sqrt{\frac{1}{4} + {sen}^{2} α - {sen}^{2} α} A = \frac{mg}{2}$

Resolução 2

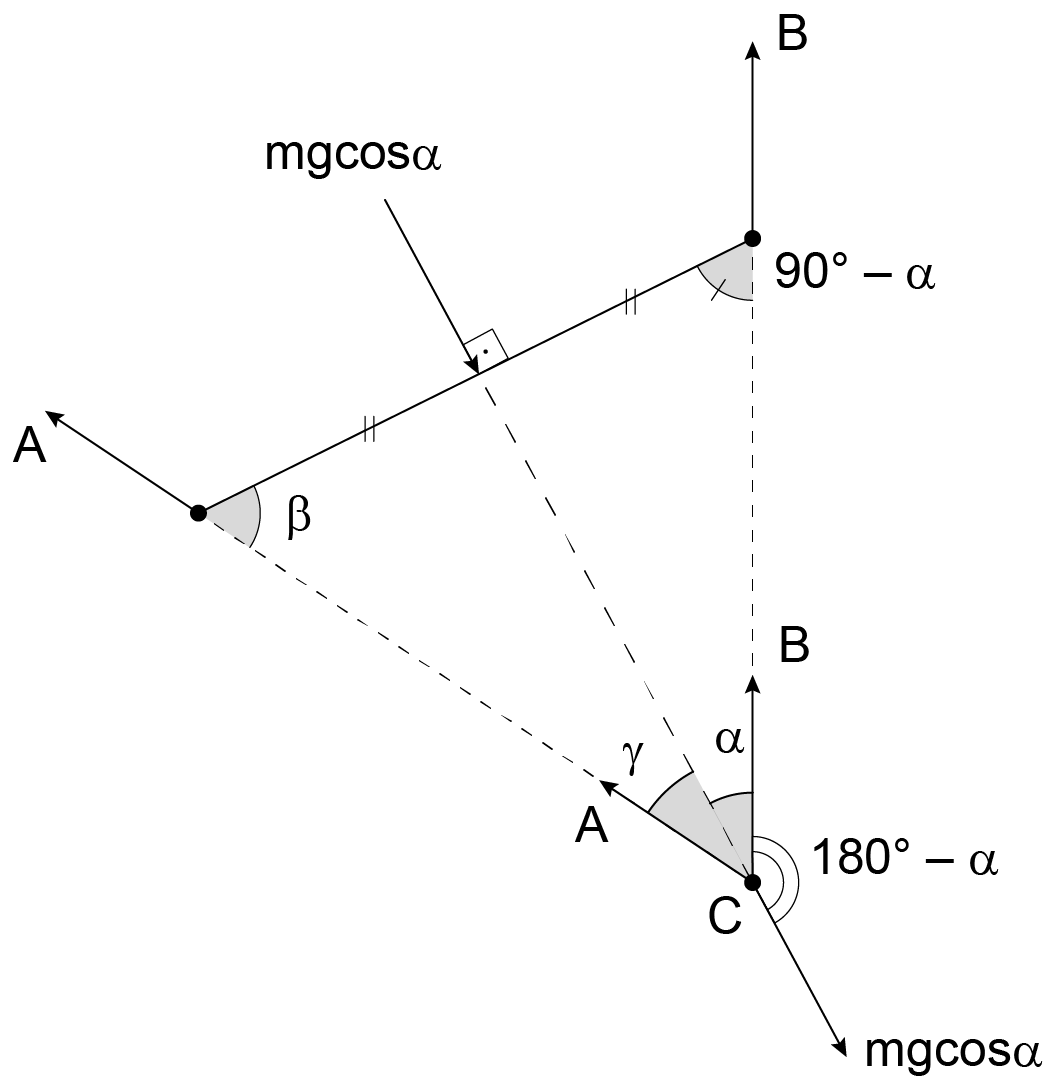
Pelo teorema das três forças, as reações A e B e a força $mg \cos α$ devem se cruzar em C.

Como a altura também é mediatriz, o $△ ABC$ é isósceles.

Logo, $β = 90^{o} - α e γ = α$

Pelo teorema de Lamy, tem-se:

$\frac{A}{sen (180^{\circ} - α)} = \frac{mg cosα}{\underset{⏟}{sen (γ + α)}} \Rightarrow \frac{A}{senα} = \frac{mg cosα}{2 senα cosα} \Rightarrow A = \frac{mg}{2}$
2

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!