Questão 8 - 1ª Fase - IME 2025

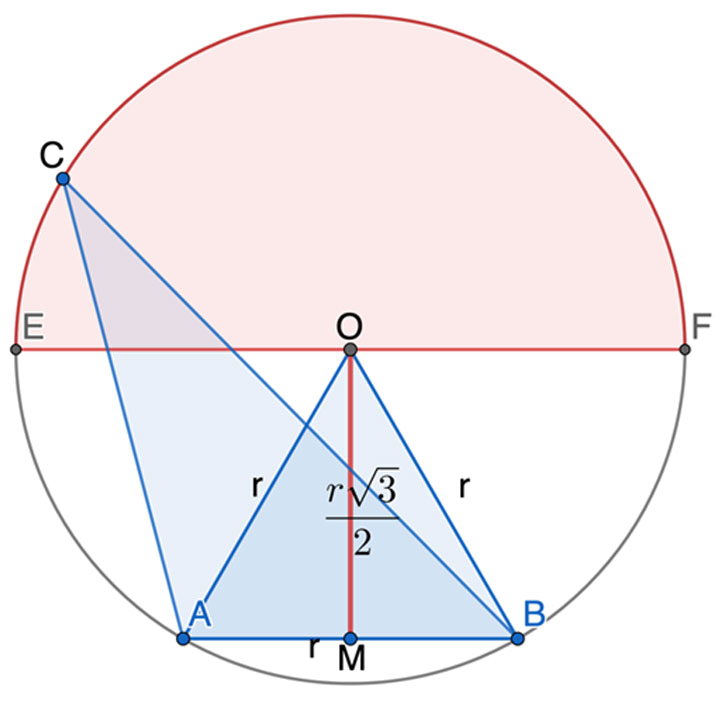
Se um triângulo ABC inscrito na circunferência de centro O e raio r tem AB = r e altura ${\mathrm{h}}_{\mathrm{c}}$, então, para que sua área seja maior que $\frac{{\mathrm{r}}^2\sqrt{3}}{4}$, tem-se:

$\frac{1}{2}·\mathrm{AB}·{\mathrm{h}}_{\mathrm{c}}=\frac{\mathrm{r}}{2}·{\mathrm{h}}_{\mathrm{c}}>\frac{{\mathrm{r}}^2\sqrt{3}}{4}\Rightarrow {\mathrm{h}}_{\mathrm{c}}>\frac{\mathrm{r}\sqrt{3}}{2}$

O valor $\frac{\mathrm{r}\sqrt{3}}{2}$ é a medida da altura do triângulo equilátero OAB. Assim, o ponto C deve recair na semicircunferência acima de $\overline{\mathrm{EF}}$, conforme a figura. 

Como o ângulo central $\mathrm{A}\hat{\mathrm{O}}\mathrm{B}$ mede 60°, o maior arco $\widehat{\mathrm{AB}}$ mede 300°. O arco da semicircunferência acima de $\overline{\mathrm{EF}}$ mede 180°. Logo, a probabilidade pedida é igual a: 

$\mathrm{p}=\frac{\mathrm{m}\left(\widehat{\mathrm{EF}}\right)}{\mathrm{m}\left(\widehat{\mathrm{AB}}\right)}=\frac{180°}{300°}=\boxed{\frac{3}{5}}$