Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

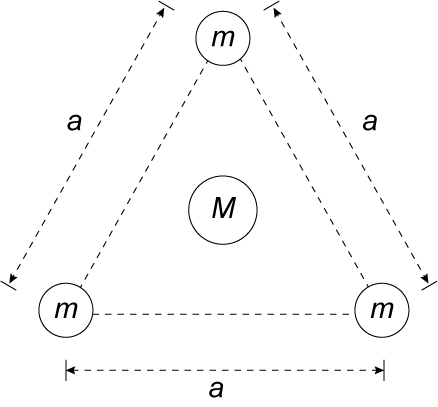
Três planetas de massas m idênticas orbitam, em trajetória circular, uma estrela de massa M. A posição relativa entre os planetas, a cada instante, forma um triângulo equilátero de lado a, conforme mostrado na figura. Sabendo que G é a constante da gravitação universal, podemos afirmar que o período dessa órbita é dado por
.
.
.
.
.
Isole-se uma das massas do triângulo equilátero:
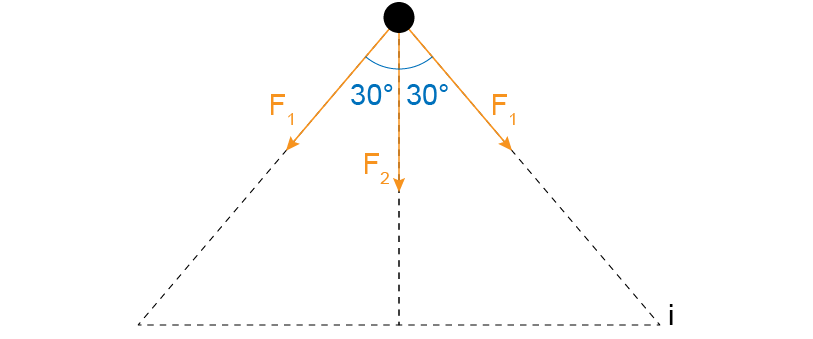
A massa fica no baricentro do triângulo equilátero e dista do vértice.
Cálculo das forças gravitacionais:
Como cada massa m descreve uma trajetória circular de raio :
Gabarito da 1ª fase do Vestibular ITA 2026
Comentários + correções ao vivo | Poliedro ResolveInscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!