Questão 21 - 1ª Fase - ITA 2026

Novidade! Correção inteligente - simulado seus resultados.

Clique aqui e veja a resolução IME 1ª Fase 2026

Clique aqui e veja a resolução ITA 1ª Fase 2026

Selecione uma prova

Gabarito

Matemática
1. 1D
2. 2B
3. 3E
4. 4C
5. 5D
6. 6A
7. 7A
8. 8B
9. 9D
10. 10E
11. 11A
12. 12B
Física
1. 13B
2. 14A
3. 15D
4. 16C
5. 17A
6. 18E
7. 19B
8. 20C
9. 21D
10. 22E
11. 23C
12. 24C
Química
1. 25A
2. 26E
3. 27D
4. 28B
5. 29E
6. 30B
7. 31E
8. 32A
9. 33B
10. 34A
11. 35A
12. 36C
Inglês
1. 37D
2. 38C
3. 39C
4. 40B
5. 41A
6. 42D
7. 43C
8. 44B
9. 45B
10. 46B
11. 47D
12. 48C

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 21

Objetiva

O circuito mostrado na figura é composto por um potenciômetro conectado a uma bateria de 12 V. Quando o cursor do potenciômetro é girado no sentido anti-horário, a resistência R1 tende a zero, e R2 atinge seu valor máximo; no sentido horário, ocorre o contrário. Um voltímetro ideal está conectado ao terminal central do potenciômetro, medindo a diferença de potencial entre esse ponto e o terminal negativo da bateria. Dois testes foram realizados nesse circuito. No Teste 1, uma resistência desconhecida R3 foi conectada, e a voltagem indicada pelo voltímetro foi registrada à medida que o cursor do potenciômetro era girado no sentido horário. No Teste 2, uma outra resistência desconhecida R4 substituiu a R3, e o procedimento foi repetido. O gráfico $V \times R 1 / R 2$ mostra os resultados obtidos nos dois testes. Com base no que foi apresentado, é possível afirmar que

Alternativas

A
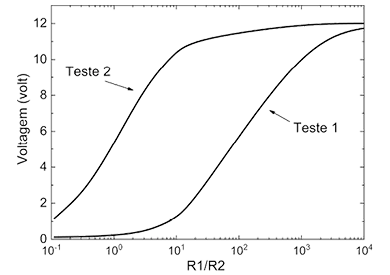
a resistência R4 é menor que a resistência R3.
B
a corrente elétrica que passa por R3 é menor do que a que passa por R4, para qualquer posição do cursor do potenciômetro.
C
a curva correspondente ficaria mais próxima à curva do Teste 1 do que à curva do Teste 2, se R3 e R4 fossem retiradas do circuito (este ramo ficaria aberto).
D
os valores da voltagem da curva $V \times R 1 / R 3$ serão menores que os valores de voltagem da curva $V \times R 1 / R 4$ para os mesmos valores de abscissa admissíveis em ambos os casos.
E
a razão entre as tensões indicadas nos Testes 2 e Teste 1 permanece constante e é exatamente igual à razão $R 4 / R 3$ , para qualquer posição do cursor do potenciômetro.

Gabarito:
D

Tomando $\frac{R_{1}}{R_{2}} = x \Rightarrow R_{1} = {xR}_{2}$

$R_{0} / / {xR}_{2} = \frac{{xR}_{2} R_{0}}{R_{0} + {xR}_{2}}$ , onde $R_{0} = R_{3} ou R_{4}$

$i = \frac{12}{R_{2} + \frac{{xR}_{2} R_{0}}{R_{0} + {xR}_{2}}} = \frac{12 (R_{0} + {xR}_{2})}{R_{2} (R_{0} + {xR}_{2}) + {xR}_{2} R_{0}}$

$V = \frac{{xR}_{2} R_{0}}{R_{0} + {xR}_{2}} \cdot i \Rightarrow V = \frac{12 \cdot {xR}_{2} R_{0}}{R_{2} (R_{0} + {xR}_{2}) + {xR}_{2} R_{0}} V = \frac{12 \cdot {xR}_{2} R_{0}}{R_{2} R_{0} + {xR}_{2}^{2} + {xR}_{2} R_{0}} \Rightarrow V = \frac{12}{\frac{1}{x} + \frac{R_{2}}{R_{0}} + 1}$

a) Do gráfico, $V_{4} > V_{3}$ :

$\Rightarrow \frac{12}{\frac{1}{x} + \frac{R_{2}}{R_{4}} + 1} > \frac{12}{\frac{1}{x} + \frac{R_{2}}{R_{3}} + 1} \Rightarrow R_{4} > R_{3} (Falsa)$

b) $i = \frac{V}{R_{0}} \Rightarrow i = \frac{1}{R_{0}} \cdot \frac{12}{(\frac{1}{x} + \frac{R_{2}}{R_{0}} + 1)}$

Se $i_{3} < i_{4} \Rightarrow \frac{12}{R_{3} (\frac{1}{x} + \frac{R_{2}}{R_{3}} + 1)} < \frac{12}{R_{4} (\frac{1}{x} + \frac{R_{2}}{R_{4}} + 1)}$

$\Rightarrow \frac{R_{4}}{x} + R_{2} + R_{4} < \frac{R_{3}}{x} + R_{2} + R_{3} \Rightarrow R_{4} < R_{3}$

Como já vimos que $R_{4} > R_{3} \Rightarrow (Falsa)$

c) Circuito aberto $R_{0} \to \infty \Rightarrow V \to \frac{12}{\frac{1}{x} + 1}$

Como o denominador diminui: $V > V_{2} > V_{1}$ , o que deixa o gráfico mais próximo do Teste 2. (Falsa)

d) $V = \frac{12}{\frac{1}{x} + \frac{R_{2}}{R_{0}} \cdot \frac{R_{1}}{R_{1}} + 1} = \frac{12}{\frac{1}{x} + \frac{R_{1}}{R_{0}} \cdot \frac{1}{x} + 1}$

$V_{3} < V_{4}$ para x fixo $\Rightarrow \frac{12}{\frac{1}{x} (1 + \frac{R_{1}}{R_{3}}) + 1} < \frac{12}{\frac{1}{x} (1 + \frac{R_{1}}{R_{4}}) + 1}$

$\frac{1}{x} + \frac{1}{x} \cdot \frac{R_{1}}{R_{4}} + 1 < \frac{1}{x} + \frac{1}{x} \cdot \frac{R_{1}}{R_{3}} + 1 \Rightarrow R_{3} < R_{4} (OK!)$

e) $\frac{V_{4}}{V_{3}} = \frac{\frac{1}{x} + \frac{R_{2}}{R_{3}} + 1}{\frac{1}{x} + \frac{R_{2}}{R_{4}} + 1} \neq \frac{R_{4}}{R_{3}} \Rightarrow (Falsa)$

Vídeos

Gabarito da 1ª fase do Vestibular ITA 2026

Comentários + correções ao vivo | Poliedro Resolve

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

Questão 21 - 1ª Fase - ITA 2026

Gabarito

Matemática

Física

Química

Inglês