Questão 17 - 1ª Fase - ITA 2026

Clique aqui e veja a resolução ITA 1ª Fase 2026

Clique aqui e veja a resolução IME 1ª Fase 2026

Novidade! Correção inteligente - simulado seus resultados.

Selecione uma prova

Gabarito

Matemática
1. 1D
2. 2B
3. 3E
4. 4C
5. 5D
6. 6A
7. 7A
8. 8B
9. 9D
10. 10E
11. 11A
12. 12B
Física
1. 13B
2. 14A
3. 15D
4. 16C
5. 17A
6. 18E
7. 19B
8. 20C
9. 21D
10. 22E
11. 23C
12. 24C
Química
1. 25A
2. 26E
3. 27D
4. 28B
5. 29E
6. 30B
7. 31E
8. 32A
9. 33B
10. 34A
11. 35A
12. 36C
Inglês
1. 37D
2. 38C
3. 39C
4. 40B
5. 41A
6. 42D
7. 43C
8. 44B
9. 45B
10. 46B
11. 47D
12. 48C

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 17

Objetiva

Considere um pêndulo simples, com um fio ideal de comprimento $l$ sob ação da gravidade de aceleração g, e um sistema massa–mola na horizontal, com uma mola de comprimento natural $x_{0}$ e uma massa que desliza sobre uma superfície lisa, conforme a figura. Ambos os corpos, o do pêndulo e o do sistema massa–mola, possuem a mesma massa. No instante inicial, o pêndulo é solto do repouso a partir de um pequeno ângulo $θ$ com a vertical, enquanto a massa do sistema massa–mola é solta também do repouso a partir de uma posição $x_{1}$ , em que a mola se encontra comprimida. As duas massas colidem quando a mola atinge seu comprimento natural e quando o pêndulo está na vertical. Nesse instante, elas possuem a mesma velocidade.

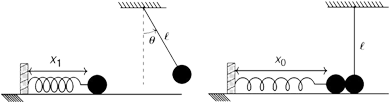
Assinale a alternativa que corresponde a relação entre o ângulo $θ$ , de lançamento do pêndulo, e os outros parâmetros físicos relevantes.

Alternativas

A
$\cos θ = 1 - \frac{{(x_{1} - x_{0})}^{2}}{2 l^{2}} .$
B
$\sin θ = 1 - \frac{{(x_{1} - x_{0})}^{2}}{2 l^{2}} .$
C
$\cos θ = 1 - \frac{{(x_{1} - x_{0})}^{2}}{l^{2}} .$
D
$\sin θ = 1 - \frac{2 l^{2}}{{(x_{1} - x_{0})}^{2}} .$
E
$\cos θ = 1 - \frac{l^{2}}{{(x_{1} - x_{0})}^{2}} .$

Gabarito:
A

1) Sistema massa-mola:

$E_{mec, in} = E_{mec, fi} \Rightarrow \frac{k {(x_{1} - x_{0})}^{2}}{2} = \frac{{mv}^{2}}{2} \Rightarrow {mv}^{2} = k {(x_{1} - x_{0})}^{2}$

2) Pêndulo simples:

$E_{mec, in} = E_{mec, fi} \Rightarrow mg l (1 - cosθ) = \frac{{mv}^{2}}{2} \Rightarrow {mv}^{2} = 2 mg l (1 - cosθ)$

Como as duas massas são iguais e elas têm a mesma velocidade na colisão:

$k {(x_{1} - x_{0})}^{2} = 2 mg l (1 - cosθ)$

Antes da colisão, cada sistema efetua um MHS com o mesmo período, logo:

$T_{1} = T_{2} \Rightarrow 2 π \sqrt{\frac{m}{k}} = 2 π \sqrt{\frac{l}{g}} \Rightarrow k = \frac{mg}{l}$

Portanto:

$\frac{mg}{l} {(x_{1} - x_{0})}^{2} = 2 mg l (1 - cosθ) \Rightarrow cosθ = 1 - \frac{{(x_{1} - x_{0})}^{2}}{2 l^{2}}$

Vídeos

Gabarito da 1ª fase do Vestibular ITA 2026

Comentários + correções ao vivo | Poliedro Resolve

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

Questão 17 - 1ª Fase - ITA 2026

Gabarito

Matemática

Física

Química

Inglês