Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!
Questão 6 - 1ª Fase - ITA 2026
Gabarito
Considere as seguintes afirmações:
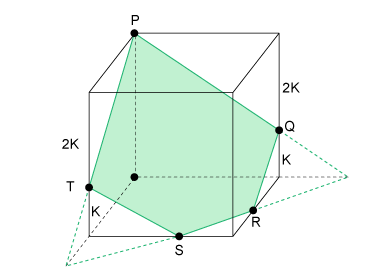
I. Um cubo possui uma seção plana dada por um pentágono.
II. Sejam , e três planos distintos, dois a dois concorrentes. Sejam r a reta interseção de e , s a reta interseção de e , t a reta interseção de e . Se r, s e t são duas a duas paralelas distintas, então existe uma única reta paralela a r que dista igualmente de , e .
III. Dois planos secantes são perpendiculares se toda reta de um deles for perpendicular ao outro plano.
É (São) VERDADEIRA(S):
Alternativas
- A
Apenas I.
- B
Apenas I e II.
- C
Apenas I e III.
- D
Apenas II e III.
- E
Nenhuma das afirmações.
Gabarito:A
I. Verdadeira. Observe figura a seguir:
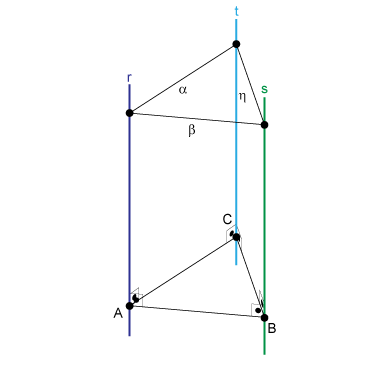
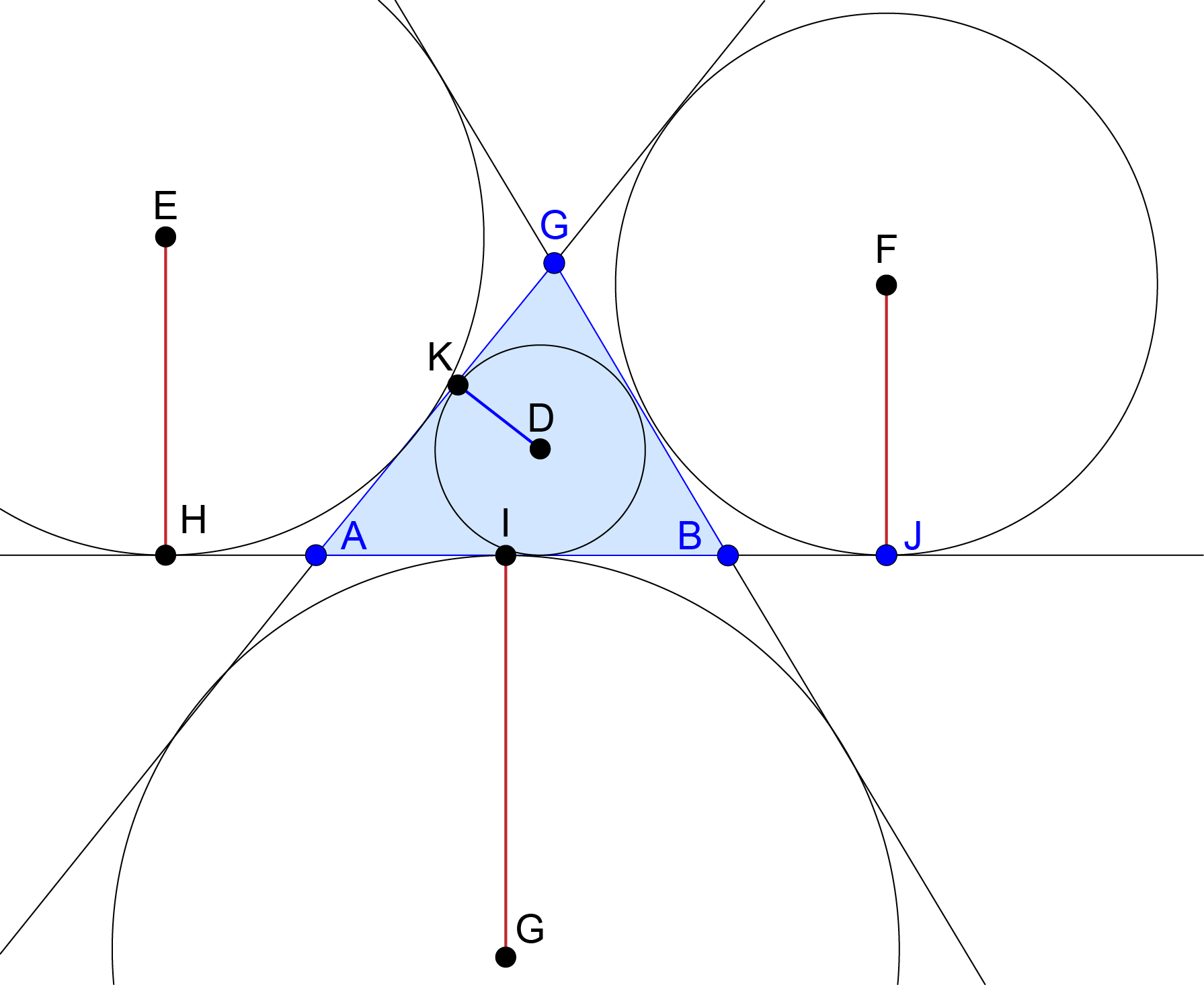
II. Falsa. Existem 4 retas equidistantes de α, β e η, todas paralelas a r,s e t. Seja um plano perpendicular às três retas r, s e t, que as intercepta nos pontos A, B e C, respectivamente (Figura 1). No plano de ABC, as retas equidistantes dos três planos têm como traço o Incentro de ABC e seus 3 exincentros, que são os pontos D, E, F e G da Figura 2.
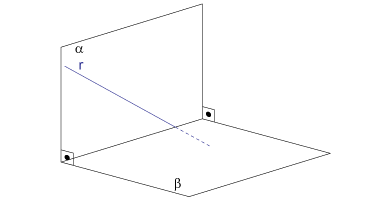
III. Falsa. Na figura α e β são perpendiculares, a reta r pertence a α, e é secante a β, sem ser perpendicular a β.
Vídeos
Gabarito da 1ª fase do Vestibular ITA 2026
Comentários + correções ao vivo | Poliedro ResolveDownloads
Provas