Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

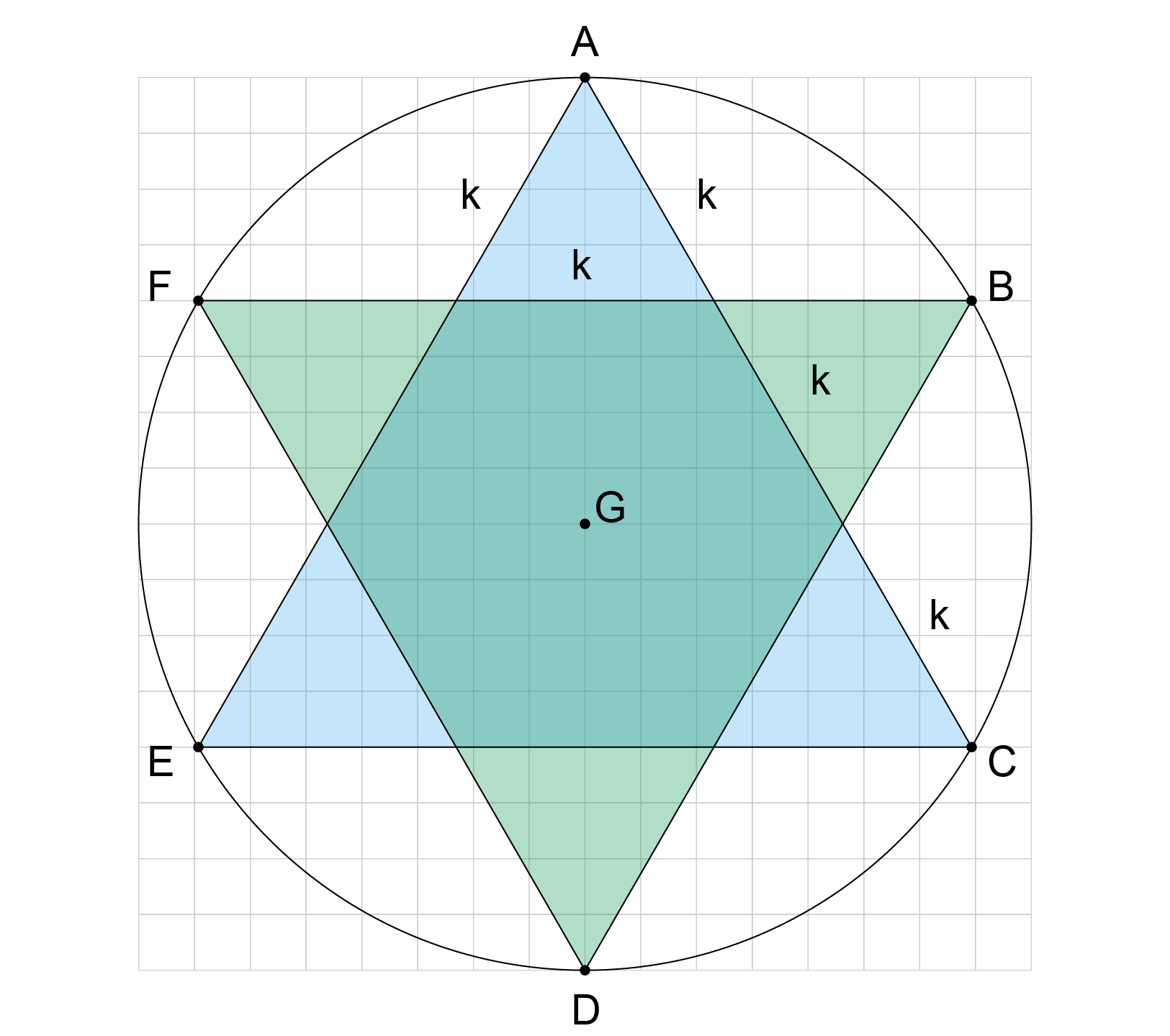
Uma circunferência é dividida em seis partes iguais pelos pontos A, B, C, D, E, F, designados nessa ordem. Os pontos A, C, E são vértices de um triângulo equilátero, os pontos B, D, F são vértices de um segundo triângulo equilátero. A sobreposição desses dois triângulos define uma estrela de seis pontas denominada hexagrama.
Se a área desse hexagrama é , então a área do quadrado inscrito na circunferência mede
.
.
.
.
.
Conforme a figura a seguir, a área de um triângulo equilátero em função do raio da circunferência circunscrita é dada por:
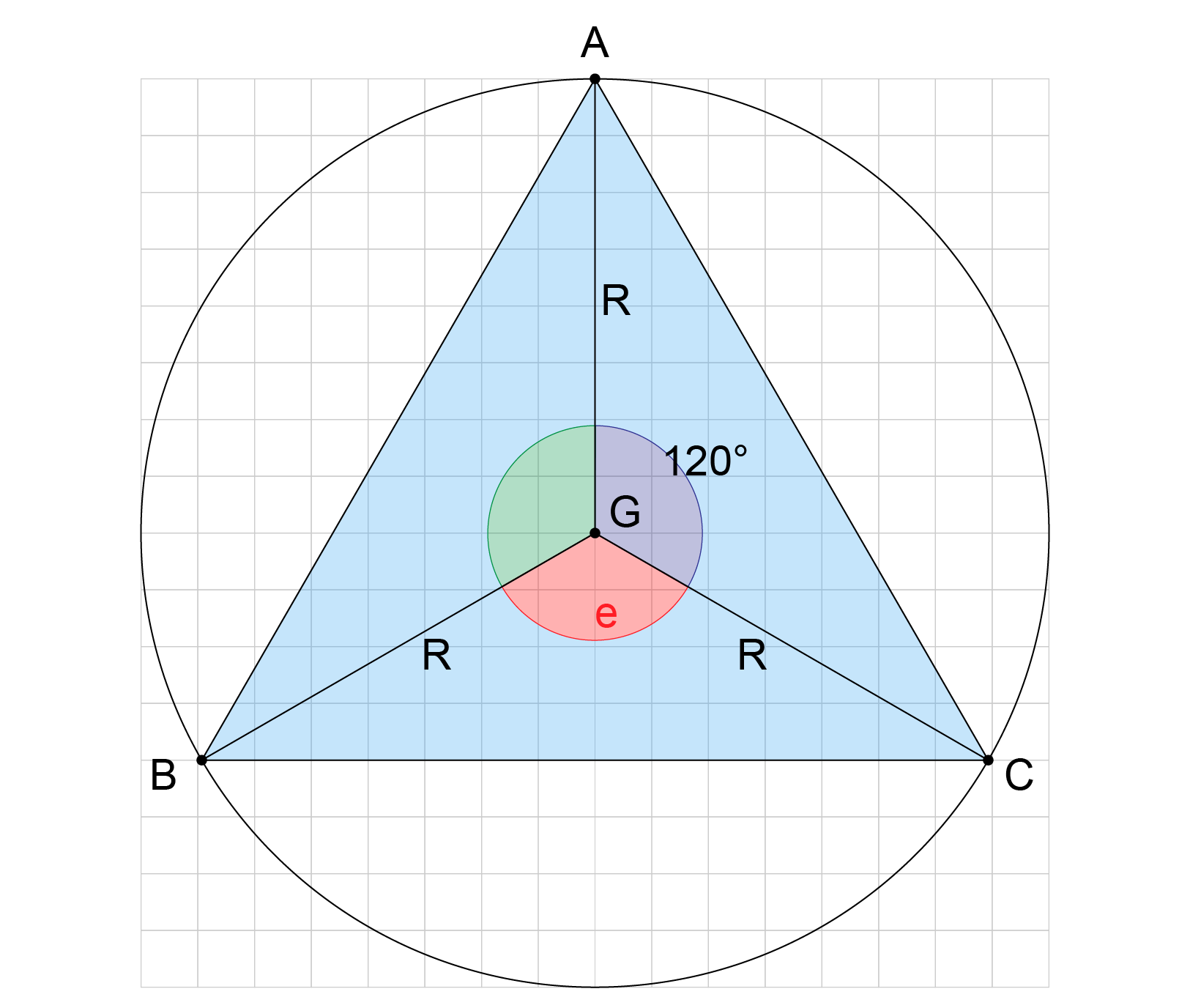
A área do hexagrama da questão pode ser calculada como a soma de um triângulo equilátero de lado 3k e 3 triângulos equiláteros de lado k, cada um com área do triângulo de lado 3k .
Logo:
A área do quadrado inscrito em uma circunferência de raio R é igual a de quatro triângulos retângulos isósceles de catetos R, conforme a figura a seguir:
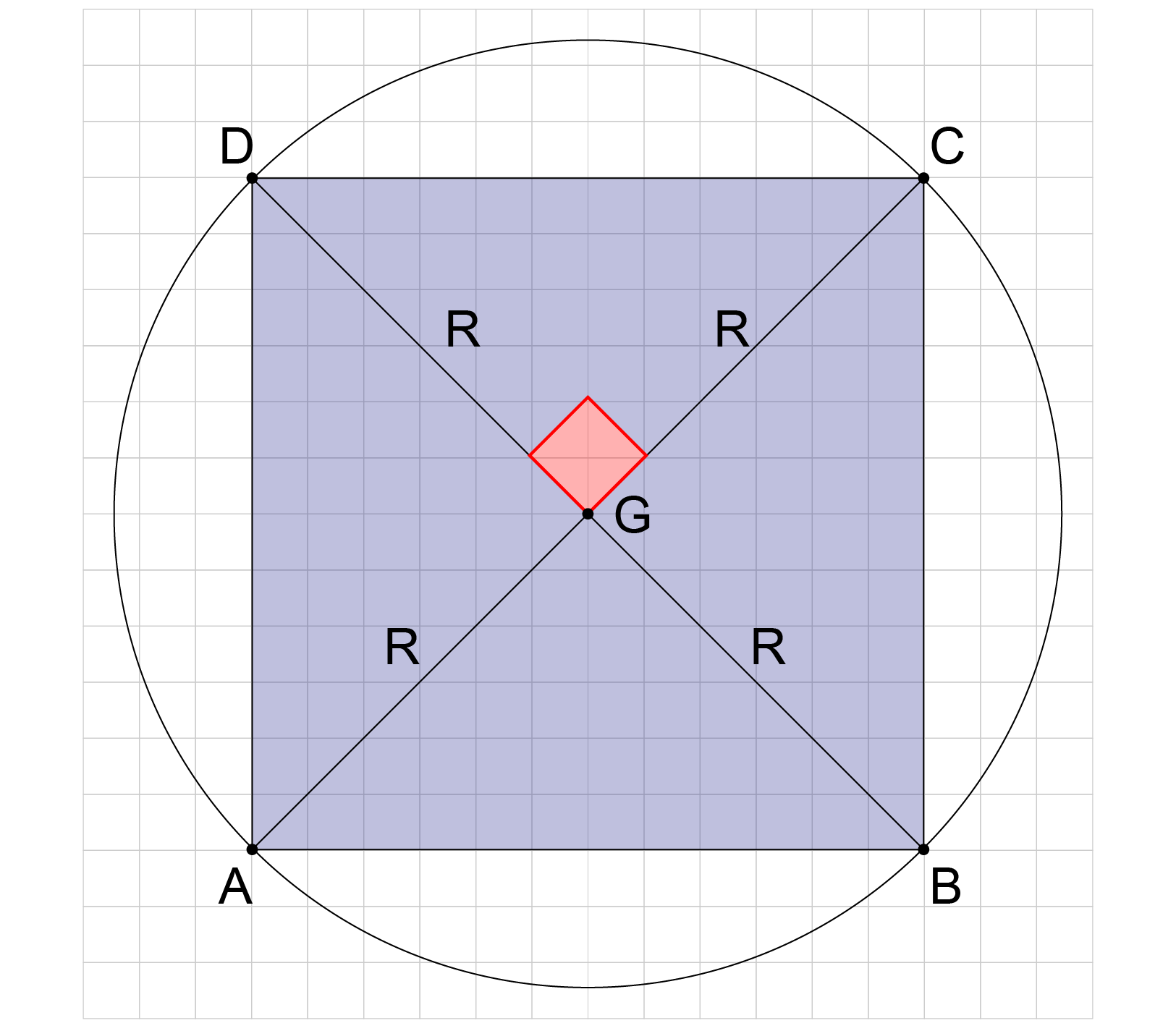
Gabarito da 1ª fase do Vestibular ITA 2026
Comentários + correções ao vivo | Poliedro ResolveInscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!